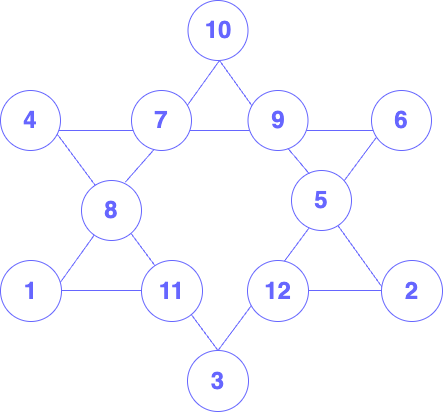
Magic Star Puzzle

Take a good look at this six-pointed figure. This is what is known as a magic star. The total in every row adds up to the same.

1+12+10+3 = 26	9 + 5 + 10 + 2 = 26
4+ 6 + 7 +9 = 26	11+ 6+ 8 + 1 = 26
4 + 8 + 12 + 2 =26	11 + 7 + 5 + 3 = 26

But there is something imperfect about this star.The sum of the numbers at the points do not add up to 26. Now can you replace the numbers in such a way that their sums in every row and every point add up to 26 ?

Now we have to see how the numbers are to be placed. Let us assume the following:
The sum of the numbers at the points is 26, while the total of all the numbers of the star is 78. Therefore, the sum of the numbers of the inner the hexagon is 78 - 26 = 52.
We shall now proceed on to examine one of the big triangles. The sum of the numbers on each of its sides is 26. If we add up the three sides we get 26 x 3 = 78. But in this case, the numbers at the points will each be counted twice. Since the sum of the numbers of the three inner pairs - i.e. the inner hexagon - must, naturally be 52. Then the doubled sum at points of each triangle is 78 - 52 = 26 or 13 for each triangle.
At this point our search narrows down. We know that neither 12 nor 11 can occupy the circles at the points. So we can try 10 and immediately we come to the conclusion that the other two digits must be 1 and 2.
It is all very simple now. All we have to do is follow up and eventually we shall find the exact arrangement we are looking for, as shown in the figure below: