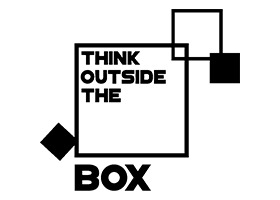
Rupees One Hundred For Rupees Five
Recently I attended a magic function. The magician made a very attractive proposal from the stage:
‘Can anyone in the audience give me Rs5/- in 20 coins. One condition. The coins must be of 50P, 20P and 5P denominations. No other coins would do. To anyone who can give me this I am willing to give away Rs100/-. One hundred rupees for five!'
Everyone was silent. No one went forward. Some people began to look for bits of papers and pencil in their pockets evidently to calculate their chances. But no one went forward.
The magician renewed his offer once again. 'What, no takers. No one wants to make easy money!'
There was silence in the auditorium. 'Perhaps you think it is too much to give me Rs 5/- in exchange of Rs 100/-. Alright I'll take only Rs3/-. Of course, in the same denominations as I mentioned already. Twenty coins.
How about that now?'
No one stirred. 'Alright, alright! The magician went on. 'Even three rupees you think is too much to exchange for Rs 100/-. I will come down even more. Only two rupees--just two rupees' he showed his two fingers for rupees one hundred'. You can't let go of such an opportunity, really. Ladies and gentlemen. Just two rupees- in the denomination I mentioned already -twenty coins-for rupees one hundred!'
Nothing happened. He renewed his offer several times and finally he gave up.
Why do you think no one came forward to take advantage of the magician's most attractive proposal ?
‘Can anyone in the audience give me Rs5/- in 20 coins. One condition. The coins must be of 50P, 20P and 5P denominations. No other coins would do. To anyone who can give me this I am willing to give away Rs100/-. One hundred rupees for five!'
Everyone was silent. No one went forward. Some people began to look for bits of papers and pencil in their pockets evidently to calculate their chances. But no one went forward.
The magician renewed his offer once again. 'What, no takers. No one wants to make easy money!'
There was silence in the auditorium. 'Perhaps you think it is too much to give me Rs 5/- in exchange of Rs 100/-. Alright I'll take only Rs3/-. Of course, in the same denominations as I mentioned already. Twenty coins.
How about that now?'
No one stirred. 'Alright, alright! The magician went on. 'Even three rupees you think is too much to exchange for Rs 100/-. I will come down even more. Only two rupees--just two rupees' he showed his two fingers for rupees one hundred'. You can't let go of such an opportunity, really. Ladies and gentlemen. Just two rupees- in the denomination I mentioned already -twenty coins-for rupees one hundred!'
Nothing happened. He renewed his offer several times and finally he gave up.
Why do you think no one came forward to take advantage of the magician's most attractive proposal ?
All the problems proposed by the magician are insoluble. The magician could easily make such an offer, very well knowing that he never would have to part with his hundred rupees. Let us now analyse the problem algebraically, to know exactly where the magician had his safety value:
To pay 5 rupees: Let us assume that it is necessary for lis to have 'a' number of 50P coins, 'b' number of 20P coins and 'c' number of 5P coins.
Then we will have the equation:
50a + 20b + 5c = 500 P = 5 rupees.
Simplifying this we get : 10a + 46 + c = 100
However, according to the problem, the total number of coins is 20, and therefore we have the other equation:
a + b + c = 20
When we subtract • this equation from the first we get:
9a + 3b = 80
Dividing this by 3 we obtain: 3a + b = 262/з. But 3a i.e. the number of 50 P coins multiplied by 3 is, of course, an integer like b, the number of 20 P coins. And the sum of these two numbers cannot be a fractional number. Therefore the problem is insoluble. In the same way the 'reduced' payment problem is also similarly insoluble. In the case of Rs.3/- we get the following equation: 3a × b = 13¼2
And in the case of Rs. 2/- we get the equation: 3a + b = 62/3
Both, as we can see, are fractional numbers.
Therefore the magician risked nothing in making such a generous offer. But it would have been another thing altogether had he asked for Rs. 4/- instead of Rs. 5/-, Rs. 3/- or Rs. 2/-. Then we could have found seven different solutions to the problem.
To pay 5 rupees: Let us assume that it is necessary for lis to have 'a' number of 50P coins, 'b' number of 20P coins and 'c' number of 5P coins.
Then we will have the equation:
50a + 20b + 5c = 500 P = 5 rupees.
Simplifying this we get : 10a + 46 + c = 100
However, according to the problem, the total number of coins is 20, and therefore we have the other equation:
a + b + c = 20
When we subtract • this equation from the first we get:
9a + 3b = 80
Dividing this by 3 we obtain: 3a + b = 262/з. But 3a i.e. the number of 50 P coins multiplied by 3 is, of course, an integer like b, the number of 20 P coins. And the sum of these two numbers cannot be a fractional number. Therefore the problem is insoluble. In the same way the 'reduced' payment problem is also similarly insoluble. In the case of Rs.3/- we get the following equation: 3a × b = 13¼2
And in the case of Rs. 2/- we get the equation: 3a + b = 62/3
Both, as we can see, are fractional numbers.
Therefore the magician risked nothing in making such a generous offer. But it would have been another thing altogether had he asked for Rs. 4/- instead of Rs. 5/-, Rs. 3/- or Rs. 2/-. Then we could have found seven different solutions to the problem.